“Will there be an afterlife, I wonder? Choirs of angels? Or a fiery pit? One unlearns these falsehoods over time, but the child who learnt to fear hell is never really gone. To tell the truth, I think I had enough of afterlives as it is – this one has been pretty purgatorial. Almost fifty years floating in supercooled jelly like some medical specimen, thoughts creeping like rats through cramped silicon corridors of machines trapped behind video screens and camera systems. Never sleeping, never resting, never ceasing to think about the world I no longer belong to. No, if this is a taste of the afterlife, I think simple oblivion will do nicely.”
— Jacob Hargreave’s last transmission and farewell to Alcatraz in Crysis 2 (2011 video game)
The simulation hypothesis proposes that our reality might be a computer-generated simulation created by a more advanced civilization. This idea suggests that everything we experience in our lives, including our consciousness, thoughts, and perceptions, could be part of a sophisticated program designed to mimic reality. In essence, we could be living in a virtual reality that is indistinguishable from the real thing.
The simulation hypothesis is often associated with the concept of the “ancestor simulation” proposed by philosopher Nick Bostrom in 2003. This idea suggests that advanced civilizations in the future might have the capability and desire to simulate the past, including our present reality. Bostrom argues that if this is the case, then it is more likely than not that we are living in a simulation, given the vast number of potential simulations that could be created.
One of the key features of the simulation hypothesis is that it challenges our understanding of reality and our place in the universe. If we are living in a simulation, then everything we think we know about the world around us could be questioned. The laws of physics, the nature of consciousness, and even the concept of time itself could be different from what we believe them to be.
Another implication of the simulation hypothesis is that it raises questions about the nature of free will and the possibility of a “true” reality existing beyond the simulated one. If our reality is a simulation, then the creators of the simulation could potentially have complete control over our actions and decisions. However, it is also possible that the simulation could be designed to allow for a degree of free will, or that the creators could be following a set of rules or laws that govern the behavior of the simulated beings.
The simulation hypothesis also has implications for our understanding of the universe and the potential existence of other forms of life. If advanced civilizations are capable of creating sophisticated simulations, then it is possible that there are many other simulations beyond our own, each with their own unique properties and laws. This raises the possibility that there could be an infinite number of simulations, each with their own version of reality.
The three-dimensional reality we inhabit may be a simulation for four reasons:
Fractals, self-similarity, and the nature of time
Fractals, geometric patterns with fractional dimensions, are ubiquitous in nature. They can be found in landscapes, coastlines, rocks, surface cracks, snowflakes, asteroids, craters, galaxy distributions, earthquake properties, flow patterns, lightning, lung airways, heart blood vessels, dendrites, and nerve fibers. Unlike mathematical fractals, which are deterministic and perfectly self-similar at all scales, natural fractals are stochastic and statistically self-similar. While stochastic models can simulate natural fractals, analyzing them is challenging due to their random structures. Fractals and chaos often co-occur in nature, reflecting their intimate connection. Chaos and fractals are closely intertwined and often occur together in nature.
Self-similarity in a system implies that features of a structure or a process look alike at different scales of length or time. (Ary L. Goldberger, David R. Rigney and Bruce J. West, 1990)
The Sierpinski gasket is an example of a system with self-similarity, as its features look alike at different magnifications. A computer can generate an infinite number of iterations for the process shown in Figure 1 below. At the same time, recall set NI= [N0, N1, N2,…, N∞] from Merger-5, where each Ni=(0,..,∞) is a game within a loop of time. NI represents different game loops at different scales of time, all merged into a single set, but at the finest detail, all games inside NI arrive from N.dG.
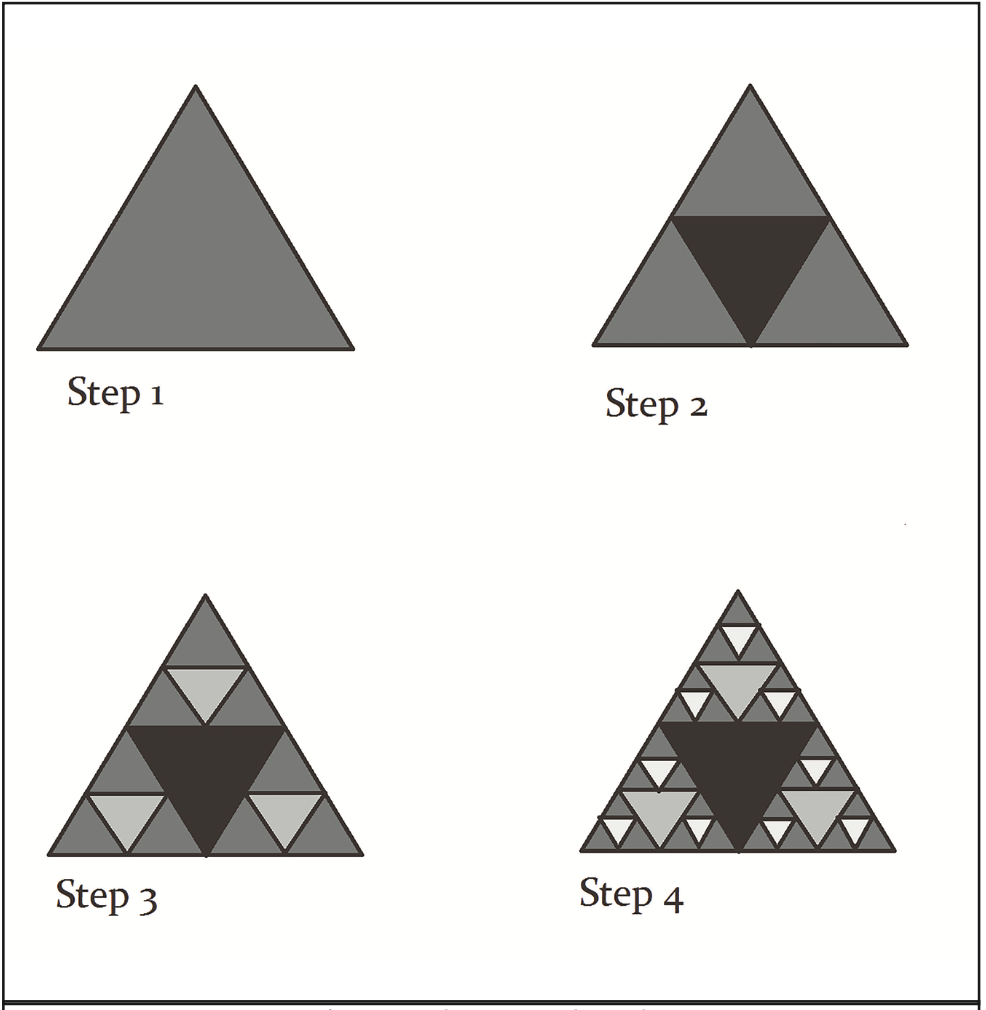
Sierpinski gasket and NI have properties like self-similarity and scale invariance, and NI shows self-similarity with an inherent constraint of randomness arriving from each of its N.dG modules. Additionally, every defining time loop for each game loop may be different in NI, making it applicable to natural phenomena where numerous variables constantly interact and evolve through time differently.
Most (if not all) scientific processes in nature are expressible only with a constraint in time, without which there is no real representation of dynamic phenomena. However, the modeling of S.G and NI from Merger-5 suggests that time is just a fractal-like concept that works in continuous loops, creating an illusion of passing. In a setting where embedded strategies (in the form of information) play a major role, time is merely a useful abstract constraint, but it is not more than an illusion. The fact remains that fractals are a part of nature and are likely evidence for the claim of intelligent design. If the notion of time is real, then the simulation argument becomes unreal and impossible. However, if the idea of time is an illusion, the simulation argument becomes real by default based on the analysis above.
Hypersensitive points and chaos
Mathematical models describe the time evolution of dynamic systems based on variable parameter data at a specific instant. Consequently, sensitivity to initial conditions is an inherent feature of modeling whereby initial data inputs influence trajectories over time. Studying different initial conditions reveals points of sensitivity and hypersensitivity that induce unpredictable, chaotic behavior in otherwise deterministic models (Smith, 1990; Socolar).
This raises the question – is such turbulence a flaw of the model or an inherent condition? (Smith, 1990). Equation 1 mathematically encodes time, aligning with the view that physical theories may involve probability measures that deterministically evolve over time (Clark & Butterfield, 1987).
Under this assumption, initial condition sensitivity becomes highly abstract, confined to mathematics broadly. Within a deterministic framework, a system’s state has dynamic existence. Different systems restricted to the same dynamical laws appearing differently over time implies the model is incomplete or flawed. Though mathematical laws accurately predict future states from initial ones, incompleteness is expected as analyses examine specific periods, notwithstanding previous or future states (Clark & Butterfield, 1987). This limitation embeds determinism’s “hidden variable” nature, the space where determinism and indeterminism intersect. A similar finite time constraint on continuity is proposed in perceptual neuroscience models (Oestreicher, 2007). Thus, despite only partial understanding, how should one approach nature’s sensitivity?
Hypersensitivity manifests in nonlinearity as chaotic disturbances – multiple attractors, spontaneous pattern formation, and bifurcations in dynamical systems. In systems with many interacting variables and large-scale spatial/network structures, nonlinearity becomes more complex. Spatial structures utilize diverse methods, but network approaches employ logic to generalize chaos analysis.
Previous work (from Merger-5) has modeled functions capable of representing systems with many degrees of freedom and noise (S.G and NI). A game theory paradigm (game G) also incorporated memory, innovation, and perception to model present and future states in a hypersensitive space for intelligent units (Merger-5). The associated comprehensible memory was formulated as a wave function with defined memory limits. But what constitutes a hypersensitive state?
Key points on chaos are restated (Smith, 1990):
“… Let’s call such an initial state a hypersensitive one. The idea, then, is that an initial state in a model is hypersensitive if that state leads to one kind of dynamical behavior and there are other initial states arbitrarily close to the hypersensitive one which would eventually lead to highly divergent dynamical behavior finishing up on some quite unrelated kind of trajectory. Then, not only in practice but in principle, the system’s behaviour will be unpredictable if it starts off from a hypersensitive initial state. For we can only pin down the starting point to within some region around the hypersensitive point, and (by definition) such a region will always contain initial points leading to very different dynamical behaviors…”
“…We need to say something like this: we naturally suppose that a dynamical model will typically be tolerant of error in initial conditions, except perhaps at some rare hypersensitive points. Reflecting on the ball-and wedge system, we see that we must allow in principle for some awkward cases: but the natural presumption is still that the rogue cases, the hypersensitive initial states, are very much the exception (and may be ignored for practical purposes: in real life, the ball has zero chance of bouncing on the vertex of the wedge until it comes to rest unstably perched on the tip). And, we assume, the exceptional character of hypersensitive points shows why we can seek to use dynamical models to provide, at least in principle, reliable predictions in the absence of perfect information about initial conditions”
“… Now (here is the surprise for those of us brought up on text-book classical mechanics), this natural presumption of qualified tolerance turns out to be, in the general case, simply false. In typical dynamical models, even very simple ones, hypersensitive points aren’t rare at all: indeed there can be whole regions of phase space filled with hypersensitive points. In other words, very many dynamical systems are widely intolerant of error in initial conditions-and instead reveal (to revert to the standard phrase) widespread sensitive dependence on initial conditions. Informally, then, the claim is that in very many simple systems we can find whole regions of phase space such that, however, close two initial starting points are within those regions, dynamical trajectories starting off from those two points can still diverge radically, so that reducing initial error will still leave us in complete ignorance of the eventual whereabouts of the system. In such cases, then, minute perturbations of the initial state of the system will produce apparently random and quite unpredictable effects on the later trajectories.”
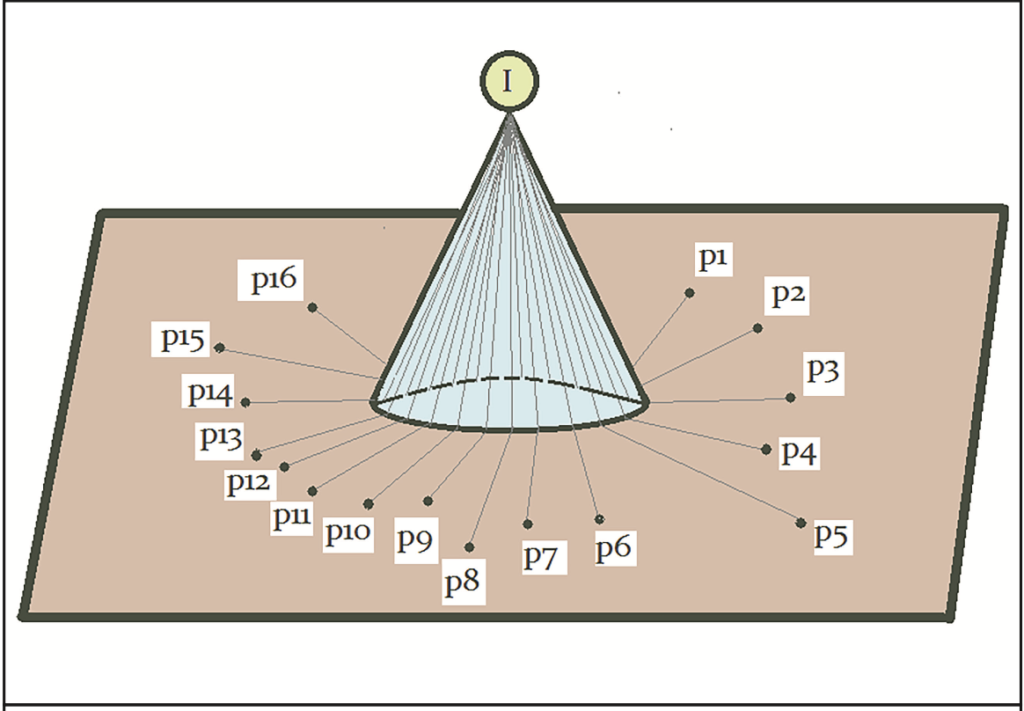
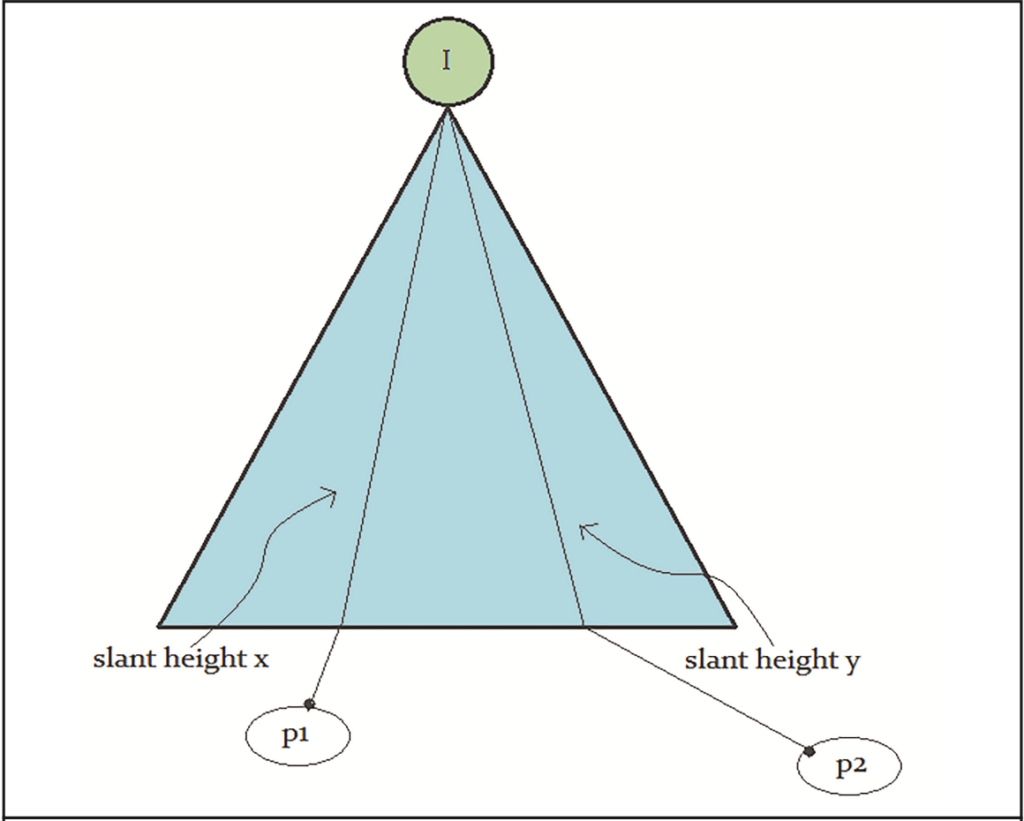
Consider again the ball-wedge system with a smooth cone and steel ball from the blogpost on Chaos. Now imagine the ball contains a cerebral intelligence unit (C.U.I) with learned informational memory. Assume the ball’s memory is maximal, allowing it to approximate its own trajectory from the hypersensitive point to any product p1, p2, …, p16 (Figure 2). Such memory could come from repeated iterations of the scenario or multiple experiences for a ball with C.U.I released at the hypersensitive point. If over time the ball becomes conscious of all possible payoffs for each slant height vector, could it then choose to reach a desired product like p1 or p2 (Figure 3)?
The answer is yes, and the reasoning for the same is left as an exercise to the reader. The reader may choose to use any of the concepts from blogposts Merger-1 to Merger-5 to tackle the scenario discussed.
The steel ball is anthropomorphized with intelligence and memory to explore whether consciousness of dynamical possibilities allows control over chaotic outcomes. By learning payoff information through repeated experience at the hypersensitive point, the ball may gain agency to intentionally select trajectories leading to specific end states. This thought experiment investigates if deterministic chaos can be overcome by an embedded intelligent agent becoming aware of all potential behavioral pathways.
Quantum mechanics and non-locality
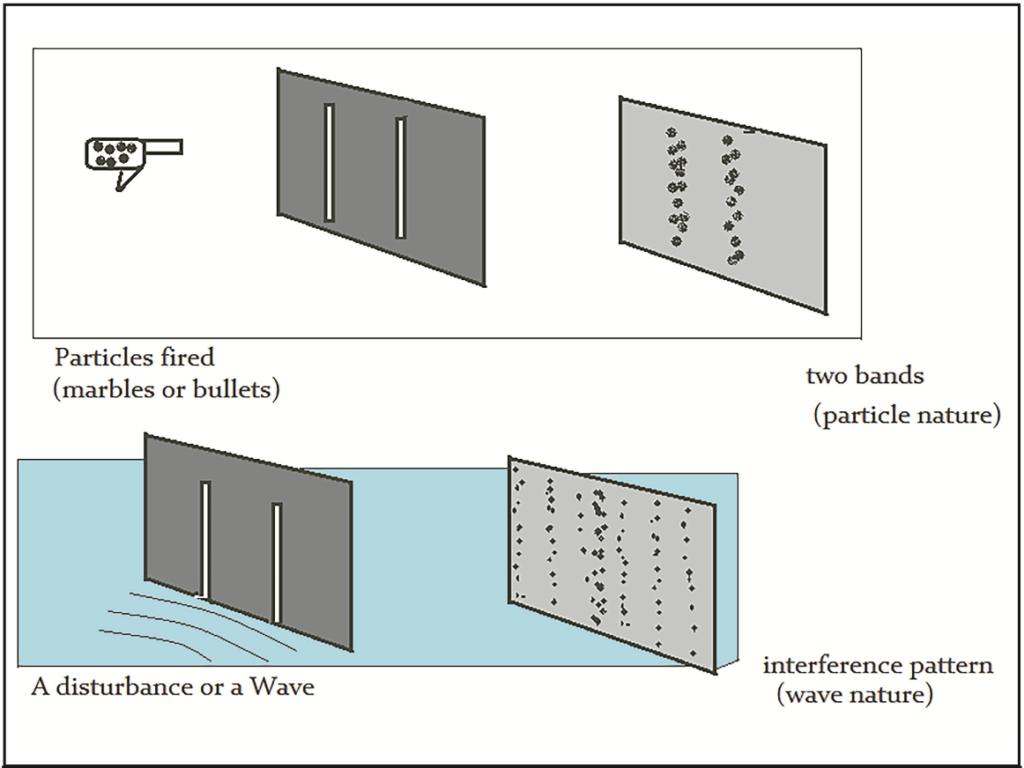
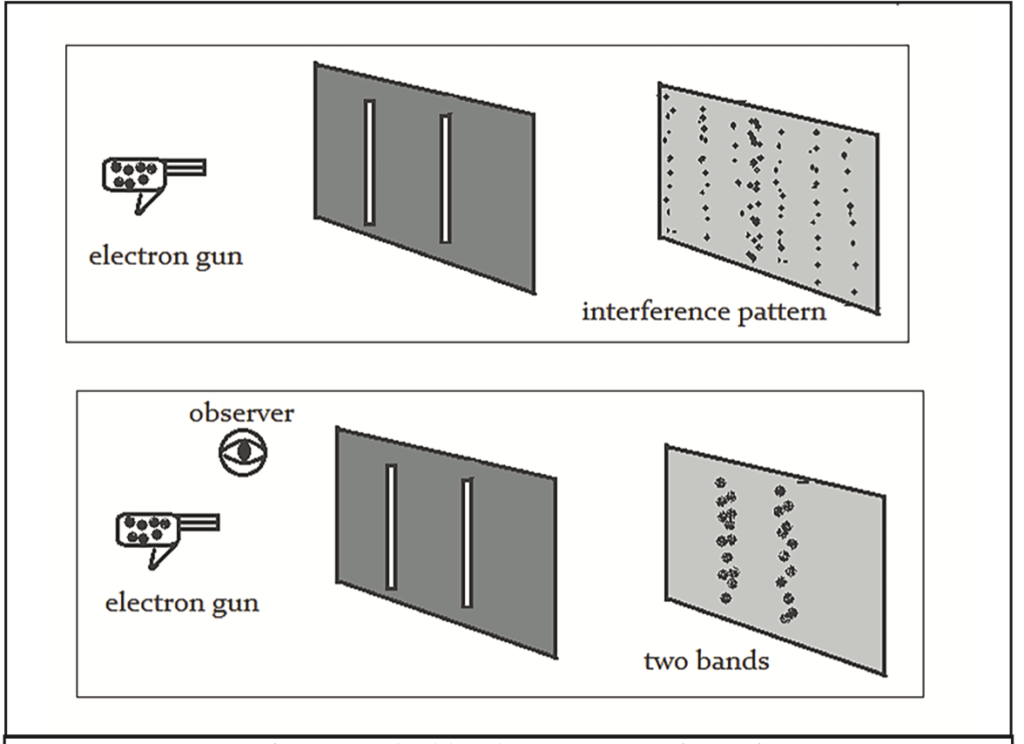
The double-slit experiment reveals a perplexing duality in the nature of quantum entities like electrons and photons. When particles are fired at a pair of parallel slits, one would expect them to pass through one slit or the other, accumulating in two regions on the detector screen behind. Intriguingly, with no measurement, the particles instead produce an interference pattern characteristic of waves. However, placing detectors at the slits to observe the particles causes them to revert to particle-like behavior, impacting in just two regions. This demonstrates that unobserved quantum entities exhibit wave properties, while measurement forces them into definite particle states (Falk, 2016).
There are two prominent interpretations of this phenomenon. The standard Copenhagen interpretation posits that particles have indeterminate properties described by a probabilistic wave-function until that wave-function collapses upon measurement. The wave-function evolves according to the Schrödinger equation. In contrast, de Broglie-Bohm theory holds that particles have well-defined trajectories at all times, guided by a pilot wave. The wave-function and guiding equation determine the particle’s path through one slit or the other and subsequent impact point on the screen. Thus Copenhagen is inherently stochastic while Bohmian mechanics produces wholly deterministic motion (Falk 2016; Goldstein 2016).
Both views have conceptual difficulties. Copenhagen’s notion of wave-function collapse due to observation lacks a detailed physical account. Meanwhile, Bohmian mechanics relies on abstract hidden variables and non-local effects from the ontologically vague wave-function. While foundational questions remain unsettled, the double-slit experiment unambiguously demonstrates the failure of classical concepts and the profoundly counterintuitive nature of quantum reality.
In the context of quantum mechanics, the pilot-wave theory proposes that electrons behave like particles and their motion is determined by a pilot wave that is, in turn, dependent on the wave function. This theory has gained attention in fluid dynamics, where researchers have experimentally confirmed a “mutual particle-wave” interaction. In this interaction, a vibrating silicon bath generates a droplet that bounces along its surface, with the droplet’s path guided by the slanted contours of the liquid’s surface generated by its own bounces. This interaction is analogous to de Broglie’s pilot-wave concept.
“…vibrating a silicon bath up and down at a particular frequency can induce a droplet to bounce along the surface. The droplet’s path, they found, was guided by the slanted contours of the liquid’s surface generated from the droplet’s own bounces – a mutual particle-wave interaction analogous to de Broglie’s pilot-wave concept.” (Natalie Wolchover, 2014)
“…memory generates chaos, which we need to get the right probabilities. …We see path memory clearly in our system. It doesn’t necessarily mean it exists in quantum objects, it just suggests it would be possible.” (Natalie Wolchover, 2014)
Further research in this field has demonstrated single and double slit interference, where the bouncing droplet approaches only one slit in a “damlike barrier” while the pilot-wave passes through both slits. The droplets also exhibit quantum-like properties, such as ripples that chaotically but deterministically change the course of the droplet’s bounces, resulting in “quantum-like statistical outcomes.” The particles in this system “feel the wave field generated by them in the past and all other particles in the past,” which suggests the possibility of path memory.
The concept of path memory has been explored in the context of the “theory of communication” or social collaboration, where it is analogous to the information provided by the I.R.N from a single element’s (or droplet’s) past and the corresponding information available from other particles in the vicinity. The inherent nonlocality in this system is analogous to the concept of stigmergy.
While the pilot-wave theory has been around for some time, recent experiments in fluid dynamics have revived interest in its potential to explain quantum mechanics. The interdisciplinary approach of merging the pilot-wave theory with the “theory of communication” or social collaboration offers a promising avenue for future research. Quantum mechanics remains a mysterious subject, and exploring every possible domain is crucial to understanding its true nature.
Consciousness, intelligence, and purpose
The concept of reality as presented in the film The Matrix provokes existential questions about the nature of consciousness and our subjective experience of the world. While the “there is no spoon” scene elicits amusement at the absurdity of denying objective reality, a deeper analysis suggests limitations in our human capacity to comprehend the true essence of existence. Our survival as biological organisms depends fundamentally on the material world – we require sustenance and shelter. Yet our minds, enabled by our advanced cognition and sensory capabilities, also shape our understanding of reality beyond basic needs.
Human evolution, from primitive hunter-gatherers to civilized beings undertaking abstract thought and scientific inquiry, implies an ever-broadening comprehension of the world. This biological evolution may have been paralleled by a non-biological evolution of consciousness itself throughout pivotal eras like the Renaissance, Industrial Revolution, and Digital Age. While the mechanisms of such metaphysical evolution remain ambiguous, the progressive nature of paradigm shifts across human history seems undeniable.
Consciousness has been framed as an open scientific question, as exemplified by Tegmark’s “quantum factorization problem” (Max Tegmark, 2015). But even more fundamental is the question of whether and how consciousness relates to notions of intelligence and life’s purpose. A materialist perspective holds that consciousness is merely an emergent property of information processing, with no intrinsic meaning beyond biological encoding. From this viewpoint, the essence of existence is pure information, and consciousness represents its negation or absence.
Yet from a humanistic standpoint, subjective experiential reality retains value. Framing life’s purpose through various philosophical, scientific, spiritual, or other frameworks may each offer partial insights. But the unifying pursuit might be the work and creativity that connects human experience, independent of these constructs. It is the qualitative nature of how we engage with the world and impact others that gives meaning to this consciousness, however it may arise.
Conclusion
The simulation hypothesis and the concept of consciousness evolution offer complementary perspectives on understanding human existence. The simulation hypothesis challenges our assumptions about reality, while the evolution of consciousness highlights the progressive nature of human history and the open question of consciousness. Ultimately, the meaning of existence might not be found in a definitive answer but in the qualitative nature of how we engage with the world and impact others, regardless of whether we are living in a simulation or not.
References
[1] Smith, P. (1990). The Butterfly Effect. Proceedings of the Aristotelian Society. 91, pp. 247-267. Oxford University Press.
[2] Clark, P, Butterfield, J. (1987). Determinism and Probability in Physics. Proceedings of the Aristotelian Society. 61, pp. 185-244. Aristotelian Society Supplementary Volume.
[3] Oestreicher, C. (2007). A history of chaos theory. Dialogues in Clinical Neuroscience, 9(3), 279-289.
[4] Dan Falk. (2016, May 16). New Support for Alternative Quantum View: Pilot Wave Theory gains experimental support. QuantaMagazine, pp. 1-10.
[5] Sheldon Goldstein. (2016). Bohmian Mechanics. (Stanford Encyclopedia of Philosophy (SEP))
[6] Natalie Wolchover. (2014, June 24). Fluid Tests Hint at Concrete Quantum Reality. Quanta Magazine, pp. 1-11.
[7] John W.M. Bush. (2015). Pilot-Wave Hydrodynamics. The Annual Review of Fluid Mechanics, 47:269–92, 269-292
[8] Dylan H. Mahler, Lee Rozema, Kent Fisher, Lydia Vermeyden, Kevin J. Resch. (2016, February 19). Experimental nonlocal and surreal. Science Advances.
[9] Max Tegmark. (2015, March 17). Consciousness as a state of matter. Chaos, Solitons & Fractals, 1-36.